Lindley's paradox

Lindley's paradox is a counterintuitive situation in statistics in which the Bayesian and frequentist approaches to a hypothesis testing problem give opposite results for certain choices of the prior distribution. The problem of the disagreement between the two approaches was discussed in Harold Jeffreys' textbook^[1]; it became known as Lindley's paradox after Dennis Lindley called the disagreement a paradox in a 1957 paper^[2].

1 Description of the paradox
2 Numerical example
- 2.1 Bayesian approach
- 2.2 Frequentist approach
3 Notes
4 References

Description of the paradox

Consider a null hypothesis H₀, the result of an experiment x, and a prior distribution that favors H₀ weakly. Lindley's paradox occurs when

The result x is significant by a frequentist test, indicating sufficient evidence to reject H₀, say, at the 5% level, and
The posterior probability of H₀ given x is high, say, 95%, indicating strong evidence that H₀ is in fact true.

These results can happen at the same time when the prior distribution is the sum of a sharp peak at H₀ with probability p and a broad distribution with the rest of the probability 1 − p. It is a result of the prior having a sharp feature at H₀ and no sharp features anywhere else.

Numerical example

We can illustrate Lindley's paradox with a numerical example. Let's imagine a certain city where 49,581 boys and 48,870 girls have been born over a certain time period. The observed proportion (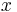 $\textstyle x$ ) of male births is thus 49,581/98,451 ≈ 0.5036. We are interested in testing whether the true proportion ( 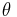$\textstyle\theta$ ) is 0.5. 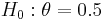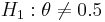That is, our null hypothesis is $\textstyle H_0: \theta=0.5$ and the alternative is $\textstyle H_1: \theta\neq0.5$ .

Bayesian approach

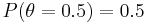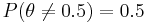We have no reason to believe that the proportion of male births should be different from 0.5, so we assign prior probabilities $\textstyle P(\theta=0.5)=0.5$ and $\textstyle P(\theta\neq0.5)=0.5$ , the latter uniformly distributed between 0 and 1. The prior distribution is thus a mixture of point mass 0.5 and a uniform distribution 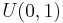$\textstyle U(0,1)$ . The number of male births is a binomial variable with mean 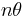$\textstyle n\theta$ and variance 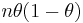$\textstyle n\theta(1-\theta)$ , where 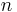$\textstyle n$ is the total number of births (98,451 in this case). Because the sample size is very large, and the observed proportion is far from 0 and 1, we can use a normal approximation for the distribution of 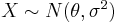$\textstyle X \sim N(\theta, \sigma^2)$ . Because of the large sample, we can approximate the variance as 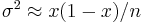$\textstyle \sigma^2\approx x(1-x)/n$ . The posterior probability is

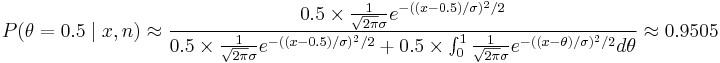$P(\theta=0.5 \mid x,n)\approx \frac{0.5\times \frac{1}{\sqrt{2\pi}\sigma}e^{-((x-0.5)/\sigma)^2/2}}{0.5\times \frac{1}{\sqrt{2\pi}\sigma}e^{-((x-0.5)/\sigma)^2/2} %2B 0.5\times\int_0^1\frac{1}{\sqrt{2\pi}\sigma}e^{-((x-\theta)/\sigma)^2/2}d\theta}\approx 0.9505$ .

So we find that there is not enough evidence to reject 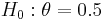$\textstyle H_0:\theta=0.5$ .

Frequentist approach

Using the normal approximation above, the upper tail probability is

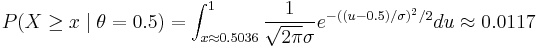$P(X \geq x \mid \theta=0.5) = \int_{x\approx 0.5036}^1\frac{1}{\sqrt{2\pi}\sigma}e^{-((u-0.5)/\sigma)^2/2}du \approx 0.0117$ .

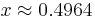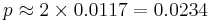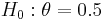Because we are performing a two-sided test (we would have been equally surprised if we had seen 48,870 boy births, i.e. $\textstyle x\approx 0.4964$ ), the p-value is $\textstyle p \approx 2\times 0.0117 = 0.0234$ , which is lower than the significance level of 5%. Therefore, we reject $\textstyle H_0:\theta=0.5$ .

The two approaches—the Bayesian and the frequentist—are in conflict, and this is the paradox.

Notes

^ Jeffreys, Harold (1939). Theory of Probability. Oxford University Press. MR 924.
^ Lindley, D.V. (1957). "A Statistical Paradox". Biometrika 44 (1–2): 187–192. doi:10.1093/biomet/44.1-2.187.

References

Shafer, Glenn (1982). "Lindley's paradox". Journal of the American Statistical Association 77 (378): 325–334. doi:10.2307/2287244. JSTOR 2287244. MR 664677.